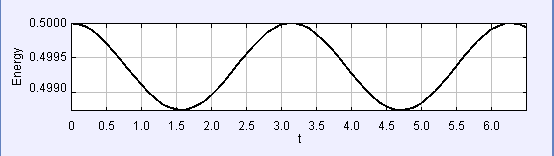
[The total SHO energy fluctuates when the model is solved using the Verlet method.]

[The total SHO energy fluctuates when the model is solved using the Verlet method.]
In order to begin our study of the numerical solution of ordinary differential equations, we model a mass on a spring using a Hooke's Law approximation to the spring force. Although the analytic solution to this simple harmonic oscillator is well known, it pays to begin with a model with a known analytic result so that we can compare this result with various numerical approximations.
The SHO Numerical Methods Model displays the analytic and numerical time evolution of a simple harmonic oscillator and the SHO total energy. The model evolves according Newton's Second Law written as two first order differential equations.
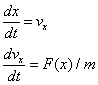
This model will be used to test various numerical approximations.
The simplest numerical method is Euler's method as described in the second model. This numerical method is not recommended because the numerical error grows quickly and a very small time steps are required. Better algorithms are easy to imagine and are easy to justify using simple mathematical and physical arguments. The Verlet algorithm, for example, computes the initial acceleration and then updates the position assuming that this acceleration is constant. The estimated position at t+Δt at then used to estimate final acceleration and average of the initial and final acceleration is used to update the velocity.
// implementation of the Verlet algorithm double a1=-k*x/m; // initial acceleration x += vx*dt + 0.5*a1*dt*dt; // advance position double a2=-k*x/m; // final acceleration vx += 0.5*(a1+a2)*dt; // advance velocity t += dt; // advance time
Note to students: The efficiency of this code can be improved by replacing k/m with a constant and by storing the final acceleration in a global variable. The final acceleration is, of course, the initial acceleration during the next time step.
Run the model and observe how each algorithm affects the position and energy. Although it may appear that we should always use the algorithm with lowest error, this may not be the case. A three-dimensional system of N particles has N2/2 pair-wise interactions and the force (acceleration) computation can be computationally difficult. A simple algorithm that conserves energy may be better than a complicated algorithm that computes the force many times and has a small energy drift, particularly if we are interested in thermodynamic quantities that do not require a detailed knowledge of particle trajectories. For this reason, the Verlet algorithm is widely used in many-particle molecular dynamics simulations.
The order of a numerical method is a measure of the accuracy of the solution depends on the time step Δt. Because the Euler method has an error per time step that is proportional to (Δt)2, halving the time step decreases this local error by a factor of four. Unfortunately, we also have to take twice as many step to cover the same total time so the global error is proportional to (Δt)1. The exponent in the that determines the global error over a fixed interval is the order of the algorithm. Although it is tempting to choose a very small time step to reduce error, a great many computations are required for all but the simplest models. A far better approach is to use a higher order algorithm.
Investigate and report on the order of the numerical methods presented in the SHO Numerical Methods Model. Use the SHO for some of your tests but test your conclusions using at least one other physical system. Possible physical systems are:
You should use either conservation of energy or a known analytic solution to estimate the error.
The following simple harmonic oscillator (SHO) models compare different solution techniques. These models are listed in order of complexity.
The SHO Numerical Methods Model was created by Wolfgang Christian using the Easy Java Simulations (EJS) version 4.1 authoring and modeling tool. You can examine and modify a compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open Ejs Model" from the pop-up menu. You must, of course, have EJS installed on your computer.
Information about Ejs is available at: <http://www.um.es/fem/Ejs/> and in the OSP comPADRE collection <http://www.compadre.org/OSP/>.